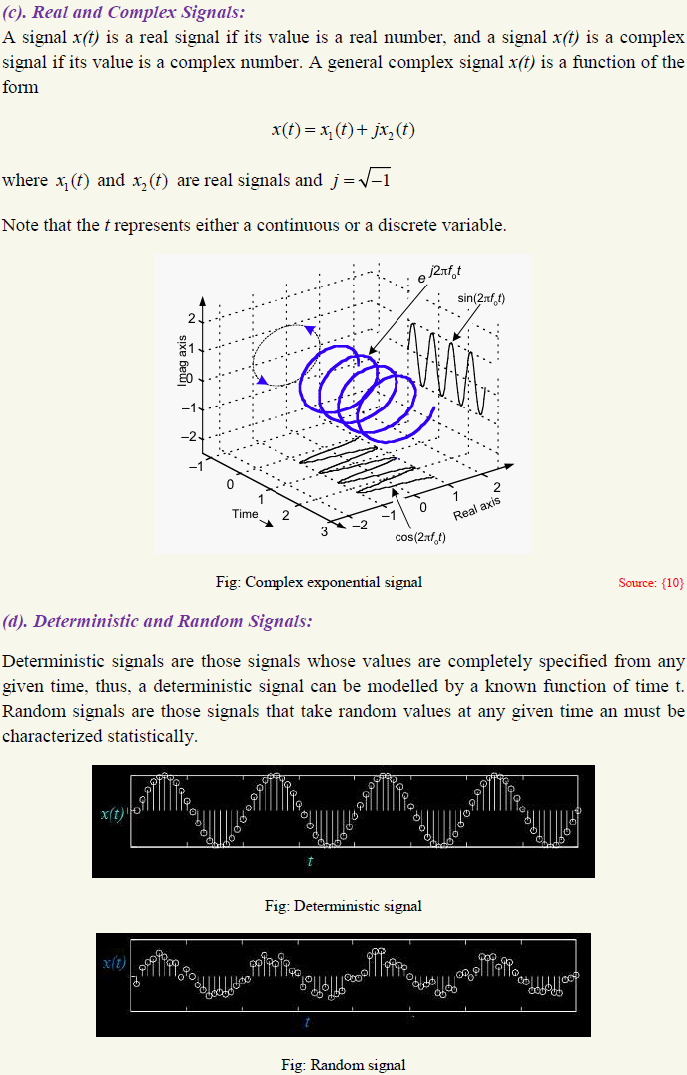
1. How can we represent signals?
Mathematically, a signal, usually is represented as a function of an independent variable time, t. Thus, a signal is denoted by x(t). A sinusoidal signal obtained from oscilloscope can be represent in following form
x(t) = xmaxsin(ω t + φ)
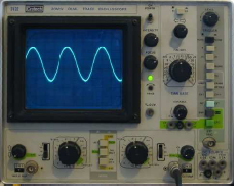
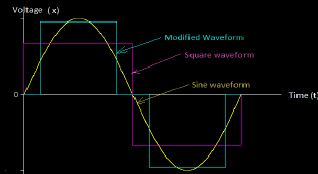
Fig: Representation of different signals obtained from oscilloscope
To represent a sinusoidal signal we require three parameters that are maximum amplitude , angular frequency and phase. Frequency (f) represent the how often signal goes through repeated cycles, i.e. ω = 2 π f. For example if the signal repeats in T (time period) second then the frequency (in Hz) will be
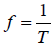
Phase is a fraction of cycle which is elapsed from an arbitrary point. For example, has delayed by 1/4th of its cycle then it becomes
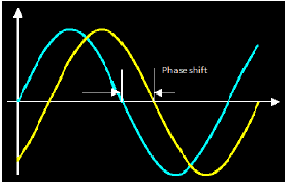
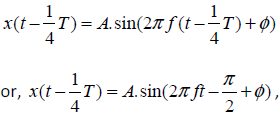
whose "phase" is now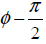
It has been shifted by 
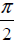radians.
2. How can we classify the signals?
The general classification of signals is classified into following categories
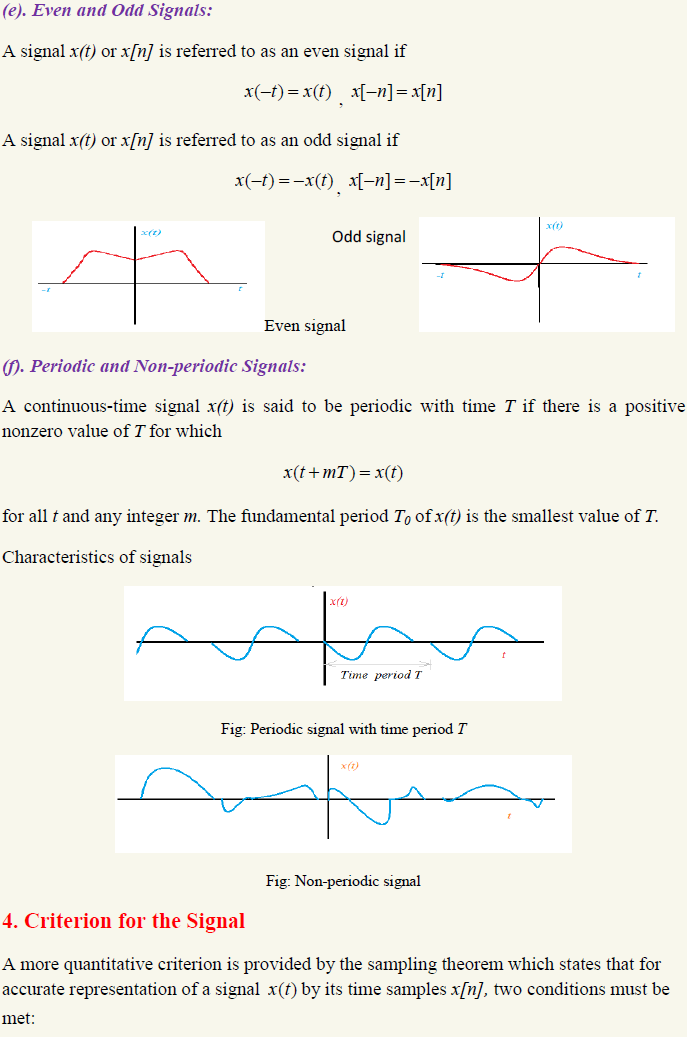
(a). Continuous-Time and Discrete-Time Signals:
A Signal x(t) is a Continuous-Time signal if it is a continuous variable. If t is a discrete variable, that is, x(t) is defined at discrete times, then x(t) is a discrete-time signal . Since a discrete-time signal is defined at discrete times, a discrete-time signal is often identified as a sequence of numbers, denoted by {xn} or x[n] where n = integer.
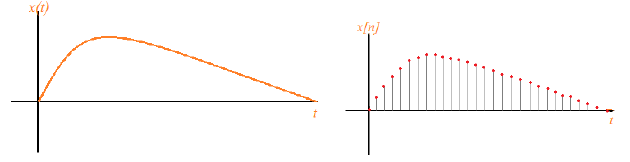
Fig: Continuous signal (takes values in the set [0, 30]) Discrete signal (takes values at the integers {0,1,...., 30})
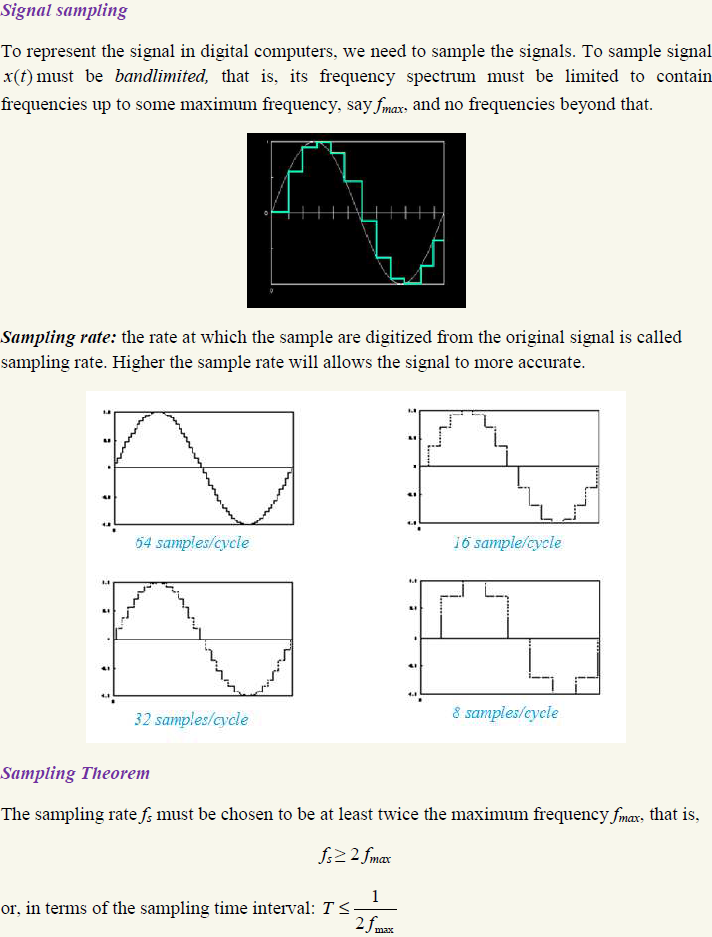
(b). Analog and Digital Signals:
If a continuous-time signal x(t) can take on any value in the continuous interval (a,b), where a may be -? and b may be +?, then the continuous-time signal x(t) is called an analog signal. If a discrete-time signal x[n] can be take on only a finite number of distinct values, then we call this a digital signal.
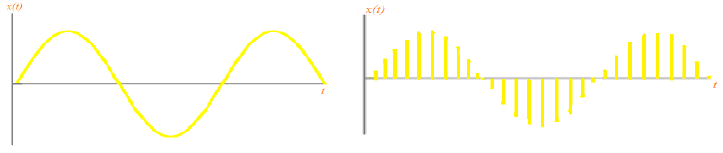
Fig: (a) Analog and (b) digital signal
