Objectives
The experiment can be used to evaluate response of first and second order mechanical systems to different type of excitations.
Introduction
By analysing the response of a system to some known excitation, the order of the system can be determined. These responses and excitaions are functions of time, Hence dynamic.
Modelling
The model of single input single output linear system, shown in the following figure,is used for the study of system dynamics.

The system equations are :

where x is the input or excitation, y is the output and G is operator or transfer function.The equation 2 is the system equation in differential form and the equation 3 in the transfer equation form.
Simplified Mechanical Systems
The basic elements of the mechanical system consists of mass, damping and some form of equilibrium restoring element, such as spring.Following figure shows the mechanical system composed of the mass-spring-damper system.
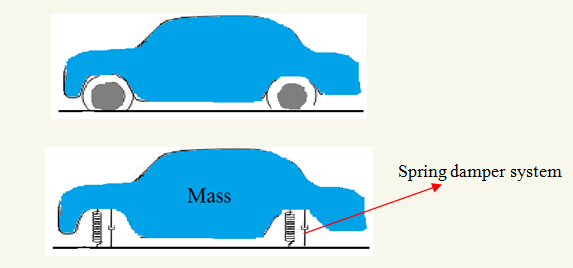
Mass
It is obvious that in all the cases mass will be a factor.Under certain condition, however, the masses making up the device or system will not affect its performance.But its very nature, mass must be distributed throughout some volume.In many cases, however, it is not only convienient but also correct, or nearly so, to assume that the mass of the member and its application, the point of concentration may or may not be center of gravity.In certain cases, the center of percussion may be the location of effective concentration.
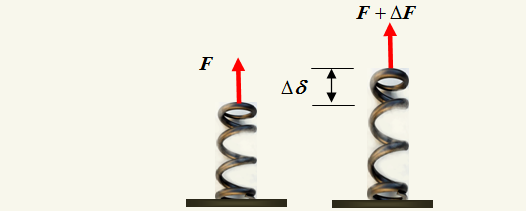
Spring Force
Many mechanical members deflect in direct proportion of the force exerted on them, that is, ΔF/Δδ=k=constant, where ΔF is an applied force increment and Δδ is the resulting deflection increment.It may be noted that the force is opposed to the deflection, that is,the resulting force always attempts to restore equilibrium.
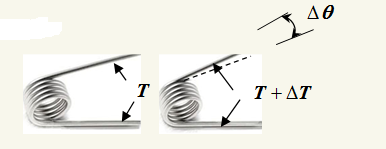
Torsional members commonly adhere to the relationship ΔT/Δθ = kt=constant, where ΔT is the applied torque increment and Δθ is the resulting torsional deflection increment.The constants k and kt are called spring constant.
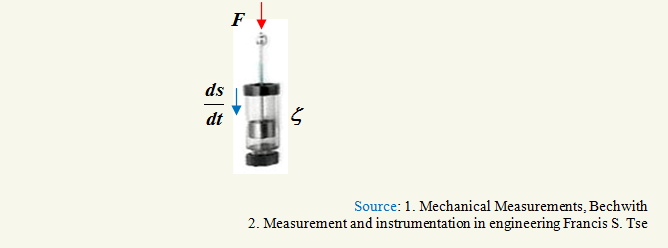
Damping
Another factor important to the usefulness of any system of this type is damping.Damping is usually thought of as viscous, rather than coulomb or frictional and may be obtained by fluids or by electrical means.
Viscous damping is a function of velocity and the force opposing the motion may be expressed as.
F = -ζ ds/dt,
where ζ = damping coefficient and ds/dt = velocity.We can see that the damping coefficient is an evaluation of force per unit velocity.The negative sign indicates the resulting force opposes the velocity.The effect of viscous damping on a freely vibrating single-degree-of-freedom system is to reduce the vibrational amplitudes with respect to time according to an exponential relation.