Theory
Time Frequency Analysis
Fourier transform is a common method for signal analysis. Fourier transform only focuses on frequency domain signal analysis. It cannot analyze the variations of frequency with respect to time.
Time frequency analysis deals with the spectrum utilization of non stationary signals such as speed, audio etc. Short Time Fourier Transform (STFT) is the simplest two dimensional time frequency representation created by computing the Fourier transform and using a sliding temporal window.
Short Time Fourier Transform(STFT)
By using Short Time Fourier transform (STFT) we can observe the changes in frequency with respect to time. The magnitude of STFT is called as spectrogram.
The Short Time Fourier transform (STFT) of signal x(t) using a window function g(t)is defined as.
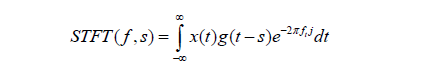
Continuous-time STFT
In continuous-time STFT, the function to be transformed is multiplied by a window function which is nonzero for only a short period of time. The Fourier transform (a one-dimensional function) of the resulting signal is taken as the window is slid along the time axis, resulting in a two-dimensional representation of the signal. Mathematically, this is written as:
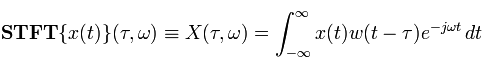
Where w(t) is the window function, commonly a Hann window or Gaussian bell centered around zero, and x(t) is the signal to be transformed. X(?,?) is essentially the Fourier Transform of x(t)w(t-?), a complex function representing the phase and magnitude of the signal over time and frequency.
Discrete-time STFT
In discrete time STFT, the data to be transformed could be broken up into chunks or frames (which usually overlap each other, to reduce artifacts at the boundary). Each chunk is Fourier transformed, and the complex result is added to a matrix, which records magnitude and phase for each point in time and frequency. This can be expressed as:
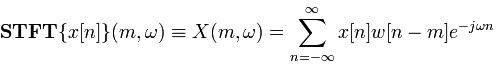
Likewise, with signal x[n] and window w[n]. In this case, m is discrete and ? is continuous, but in most typical applications the STFT is performed on a computer using the Fast Fourier Transform, so both variables are discrete and quantized.