Rotordynamic Terms
Before going to the Rotordynamic terms one must be familiar with some basic vibration terms on which whole Rotordynamic analyses depends.
Natural frequency: Natural frequency is the frequency at which a system naturally vibrates once it has been set into motion. In other words, natural frequency is the number of times a system will oscillate (move back and forth) between its original position and its displaced position, if there is no outside interference. More precisely frequencies of the free vibration are called the Natural frequencies.
Mode shape: A mode shape is an inherent dynamic property of a structure in "free" vibration (when no external forces are acting). It represents the relative displacements of all parts of the structure for that particular mode and it is associated with a particular modal frequency (natural frequency).
Basic Rotor Dynamic Terms
Whirling and critical speed
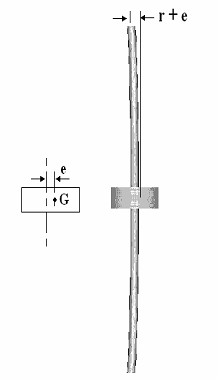
When a shaft rotates, it may well go into transverse oscillations. If the shaft is out of balance, the resulting centrifugal force will induce the shaft to vibrate and whirl about its own axis. When the shaft rotates at a speed equal to the natural frequency of transverse oscillations, i.e. critical speed this vibration becomes large and shows up as a whirling of the shaft. It also occurs at multiples of the resonant speed. This can be very damaging to heavy rotary machines such as turbine generator sets and the system must be carefully balanced to reduce this effect and designed to have a natural frequency different to the speed of rotation. When starting or stopping such machinery, the critical speeds must be avoided to prevent damage to the bearings and turbine blades.
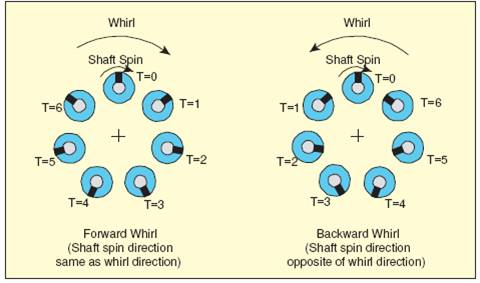
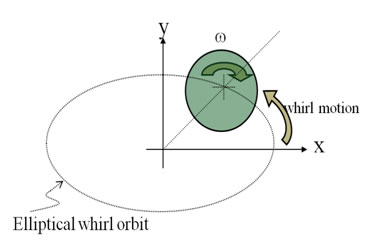
- Forward Wirl : when ω and the whirl motion are rotating in the same direction.
- Backward whirl: when ω and the whirl motion are rotating in opposite directions.
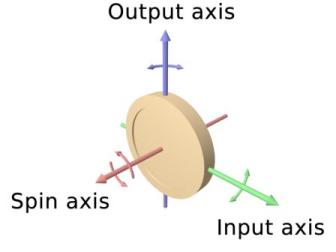
Gyroscopic effect
For a structure spinning about an axis Δ(shaft axis,spin axis), if a rotation about an axis perpendicular to Δ (a precession motion) is applied to the structure, a reaction moment appears. That reaction is the gyroscopic moment. Its axis is perpendicular to both the spin axis Δ and the precession axis.
Critical speed and Campbell diagram
The critical speed is the rotational speed that corresponds to the structure's resonance frequency (or frequencies). A critical speed appears when the natural frequency is equal to the excitation frequency. The excitation may come from unbalance which is synchronous with the rotational velocity or from any asynchronous excitation.
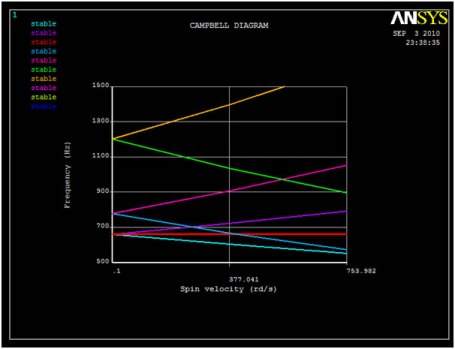
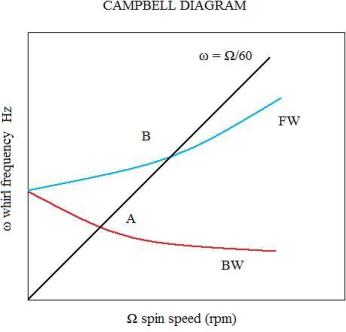

The typical rotor-bearing system has been shown in the above figure and the linearized equation of motion (dynamic equilibrium equation) with the two assumptions of small unbalance and small displacements is of the following general from:
![]()
Where q (t) is a vector containing the generalized coordinates, referred to an inertial frame, M is the symmetric mass matrix, C is the symmetric damping matrix, G is the skew-symmetric gyroscopic matrix, K is the symmetric stiffness matrix, H is the skew-symmetric circulatory matrix, and f (t) is a time-dependant vector in which all forcing functions are listed.