Modal analysis
Modal analysis is the process of determining the inherent dynamic characteristics of a system in forms of natural frequencies, damping factors and mode shapes, and using them to formulate a mathematical model for its dynamic behaviour. The formulated mathematical model is referred to as the modal model of the system and the information for the characteristics are known as its modal data.
The dynamics of a structure are physically decomposed by frequency and position. This is clearly evidenced by the analytical solution of partial differential equations of continuous systems such as beams and strings. Modal analysis is based upon the fact that the vibration response of a linear time-invariant dynamic system can be expressed as the linear combination of a set of simple harmonic motions called the natural modes of vibration. This concept is akin to the use of a Fourier combination of sine and cosine waves to represent a complicated waveform. The natural modes of vibration are inherent to a dynamic system and are determined completely by its physical properties (mass, stiffness, damping) and their spatial distributions. Each mode is described in terms of its modal parameters: natural frequency, the modal damping factor and characteristic displacement pattern, namely mode shape. The mode shape may be real or complex. Each corresponds to a natural frequency. The degree of participation of each natural mode in the overall vibration is determined both by properties of the excitation source(s) and by the mode shapes of the system.
Modal analysis embraces both theoretical and experimental techniques. The theoretical modal analysis anchors on a physical model of a dynamic system comprising its mass, stiffness and damping properties. These properties may be given in forms of partial differential equations. An example is the wave equation of a uniform vibratory string established from its mass distribution and elasticity properties. The solution of the equation provides the natural frequencies and mode shapes of the string and its forced vibration responses. However, a more realistic physical model will usually comprise the mass, stiffness and damping properties in terms of their spatial distributions, namely the mass, stiffness and damping matrices. These matrices are incorporated into a set of normal differential equations of motion. The superposition principle of a linear dynamic system enables us to transform these equations into a typical eigenvalue problem. Its solution provides the modal data of the system. Modern finite element analysis empowers the discretization of almost any linear dynamic structure and hence has greatly enhanced the capacity and scope of theoretical modal analysis. On the other hand, the rapid development over the last two decades of data acquisition and processing capabilities has given rise to major advances in the experimental realm of the analysis, which has become known as modal testing .
Modal testing
Modal testing is an experimental technique used to derive the modal model of a linear time-invariant vibratory system. The theoretical basis of the technique is secured upon establishing the relationship between the vibration response at one location and excitation at the same or another location as a function of excitation frequency. This relationship, which is often a complex mathematical function, is known as frequency response function or FRF in short. Combinations of excitation and response at different locations lead to a complete set of frequency response functions (FRFs) which can be collectively represented by an FRF matrix of the system. This matrix is usually symmetric, reflecting the structural reciprocity of the system.
.

The practice of modal testing involves measuring the FRFs or impulse responses of a structure. The FRF measurement can simply be done by asserting a measured excitation at one location of the structure in the absence of other excitations and measure vibration responses at one or more location(s). Modern excitation technique and recent developments of modal analysis theory permit more complicated excitation mechanisms. The excitation can be of a selected frequency band, stepped sinusoid, transient, random or white noise. It is usually measured by a force transducer at the driving point while the response is measured by accelerometers or other probes. Both the excitation and response signals are fed into an analyser which is an instrument responsible for computing the FRF data.
Mode Shapes
A mode shape is a deflection-pattern associated with a particular modal frequency - or pole location. It is neither tangible nor easy to observe. It is an abstract mathematical parameter which defines a deflection pattern as if that mode existed in isolation from all others in the structure.
The actual physical displacement, at any point, will always be a combination of all the mode shapes of the structure. With harmonic excitation close to a modal frequency, 95% of the displacement may be due to that particular mode shape, but random excitation tends to produce an arbitrary "shuffling" of contributions from all the mode shapes.
Nevertheless, as stated earlier, a mode shape is an inherent dynamic property of a structure in "free" vibration (when no external forces are acting). It represents the relative displacements of all parts of the structure for that particular mode.
Modes are inherent properties of a structure. They don't depend on the forces or loads acting on the structure. Modes will change if the material properties (mass, stiffness, damping properties), or boundary conditions (mountings) of the structure change. Mode shapes don't have unique values, and hence don't have units associated with them. However, mode shapes are unique. That is, the motion of one point relative to another at resonance is unique.
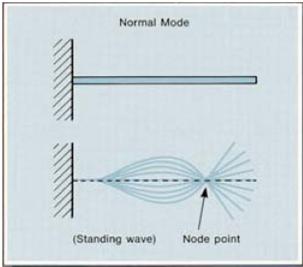
Normal modes
These are characterized by the fact that all parts of the structure are moving either in phase, or 180° out of phase,with each other. The modal displacements Ψir are therefore real and are positive or negative. Normal mode shapes can be thought of as standing waves with fixed node lines. The damping distribution in a structure determines whether the modes will be normal or complex. When a structure has very light or no damping it exhibits normal modes. If the damping is distributed in the same way as inertia and stiffness (proportional damping), we can also expect to find normal modes.
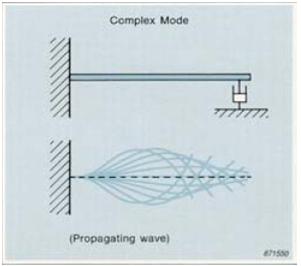
Complex modes
Complex modes can have any phase relationship between different parts of the structure. The modal displacements Ψir are complex and can have any phase value. Complex mode shapes can be considered as propagating waves with no stationary node lines. Structures with much localized damping, such as automobile bodies with spot welds and shock absorbers, have complex modes.
Mode Shape Examples Of Single Disc Rotor System :
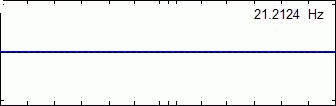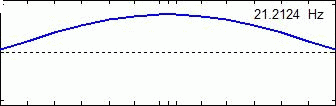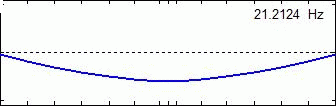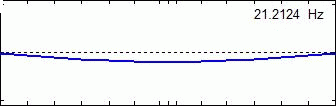

1st Mode 2nd Mode

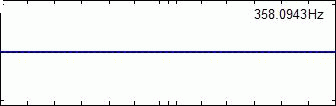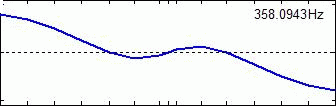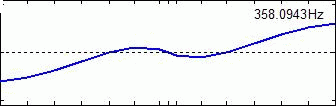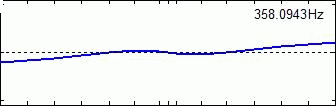
3rd Mode 4th Mode