Rotordynamics
Rotordynamics is that branch of systems dynamics dealing with mechanical devices in which at least one part, usually defined as rotor, rotates with significant angular momentum. Following the ISO definition, a rotor is a body suspended through a set of cylindrical hinges or bearings that allows it to rotate freely about an axis fixed in space.
Rotors provided with material bearings to constrain their spin axis in a more or less rigid way to a fixed position in space are usually referred to as fixed rotors, whereas those that are not constrained in any way are defined as free rotors. In the first case, the spin speed is usually considered as constant or at least as imposed by a driving device, whereas the speed of the latter is governed by the conservation of the angular momentum.
Rotordynamic analysis is not restricted to the design stage: It can supply tools that are essential during testing and actual operation of machinery and is essential to gain a deep insight of the working conditions and to perform preventive maintenance.
The study of the mechanical signature, i.e., the vibration spectrum, of a rotating machine allows us to identify operating problems even before they become dangerous and to avoid the fact that the failure of a component precipitates failure or damages to other parts. Any deviation of the signature from its usual pattern provides a symptom, in many cases easily interpreted, of a problem that is developing and allows the required countermeasures in time to be taken.
Rotordynamic analysis
Lateral rotor vibration analysis
1.Unbalance steady state response analysis -(Jeffcott rotor) :
Since the translational and rotational motions are decoupled, the translational and rotational stiffness of the elastic shaft can be obtained from the basic beam deflection equations. For the determination of translational shaft bending stiffness, consider a simply supported beam with a concentrated load a midspan (disk location). At midspan the slope is zero and the defection due to the pint load (F) is:
![]()
From the linear force-displacement relationship, the shaft bending stiffness for the fundamental translational motion is
![]()
For the determination of rotational shaft bending stiffness, consider a simply supported beam with a moment load at midspan (disk location). At midspan, the deflection is zero and the slope due to the moment (M) load is:

Again, the shaft rotation stiffness for the fundamental rotational motion is:

For the Laval- Jeffoctt rotor system, with flexible rotor and rigid bearings, the translational and rotational motion corresponds to the first second bending modes.
1.1 Equation of motion
This is the simplest 2DOFmodel of a rotor system with lateral deflection of shaft due to static unbalance. Let us suppose the centre line of shaft passes through the origin O of a rectangular coordinate system XYZ. Let the mass or geometric centre is M coincides with a shaft centre S(x, y)on shaft centreline, however sometimes it does not coincides with it, and G(x, y) is the centre of gravity which is offset from the S by e ,this eccentricity produces static unbalance . In this model it is assumed that the M is coinciding with S and then it can be shown that M and G are offset by eccentricity i.e. ![]() =e.
=e.
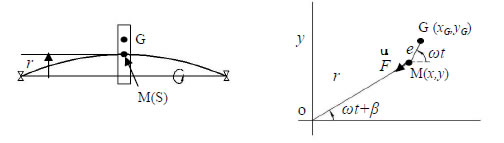
Figure 1.2 Rotor system with 2DOF for lateral vibration
Let us consider the spin velocity of rotor is Ω which also moves in a orbit about centre of shaft with the lateral deflection r, this creates unbalance force and this orbital motion is called a whirl.The restoring forces on the spring can be shown by ![]() and
and ![]() where
where ![]() and
and ![]() are the spring stiffness in x and y direction. Now the equation of motion for the undamped system is given by
are the spring stiffness in x and y direction. Now the equation of motion for the undamped system is given by  a a a a a Now we have the relation from the figure
a a a a a Now we have the relation from the figure  a a a a After substituting these relations into equation (1.1), we get
a a a a After substituting these relations into equation (1.1), we get






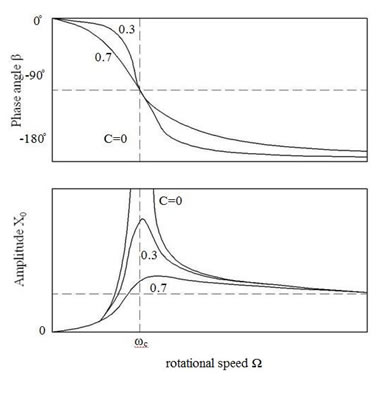
Time -Transient response analysis
Torsional rotor vibration
Stability analysis
Time -Transient response analysis
Bearing analysis
Elements of rotordynamics


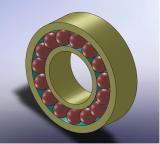
Disc Rotor or Shaft Bearing
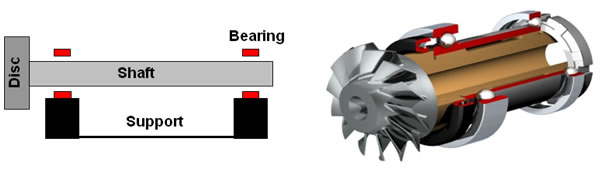
Typical Rotor-Bearing System